数据结构与算法【排序算法】

字数统计: 3k字   |   阅读时长: 12分

一、前言

在日常生活中，排序可谓是无处不在。

因此，在程序开发中，掌握排序算法也是程序员最最基本的要求了。

下面，一起来学习一下排序算法吧。

二、十大排序算法

（一）比较排序

冒泡排序、选择排序、插入排序、归并排序、快速排序、希尔排序、堆排序

（二）非比较排序

计数排序、基数排序、桶排序

（三）十大排序算法的一些参数比较

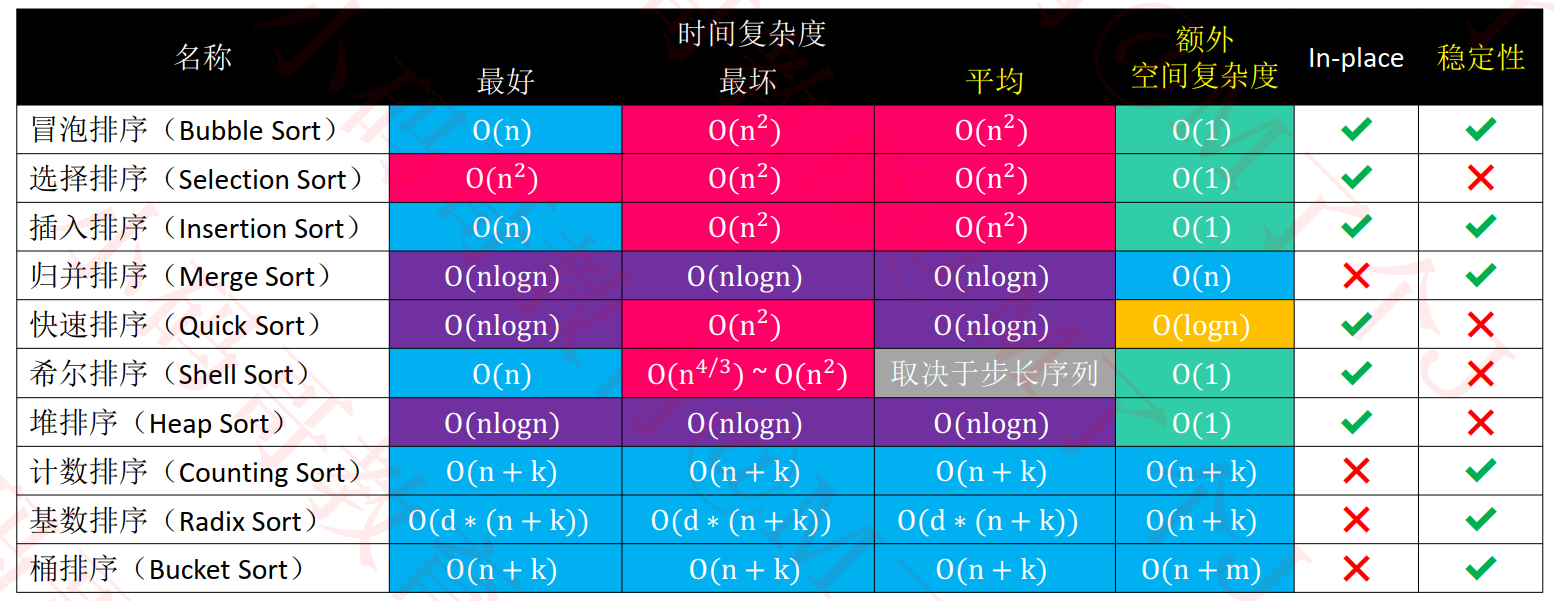
排序算法参数比较
注意：

以上表格是基于数组进行排序的一般性结论。

三、冒泡排序

注意：

本篇文章都是默认按照升序排序进行的整理，降序排序只需自己修改相关比较的代码即可。

（一）算法思想

1）从头开始，每一对相邻的元素都进行比较，如果左边的元素比右边的元素大，则两者进行交换（执行完一轮后，最末尾的元素就是最大的元素）
2）忽略1）中找到的最大元素，重复执行n-1轮，直到排序完成

（二）算法基本实现
1
2
3
4
5
6
7
8
9
10
11
int[] array =  {13, 23, 11, 79, 54, 43};
		
for(int end=array.length-1; end > 0; end--) {
    for (int begin = 1; begin <= end; begin++) {
        if(array[begin-1] > array[begin]) {
            int temp = array[begin-1];
            array[begin-1] = array[begin];
            array[begin] = temp;
        }
    }
}
（三）算法优化01
优化思路：

1）可能初始的数据就是有序的；
2）经过非常少的轮数就已经将数据排序完成。
这两种情况下，其实就没必要在比较n-1轮了，可以直接结束。
因此，在每一轮遍历的时候都先假设数据就是有序的，设置flag为true，然后如果数据在比较的过程中有经过交换（说明这一轮不是有序），则将flag修改为false。
在每一轮遍历结束后都判断flag是否为true，如果为true就说明在上一轮的比较交换之后，数据就已经变成有序的了，因此 直接停止比较；否则继续遍历。

代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int[] array =  {13, 23, 11, 79, 54, 43};
		
for(int end=array.length-1; end > 0; end--) {
    boolean flag = true;
    for (int begin = 1; begin <= end; begin++) {
        if(array[begin-1] > array[begin]) {
            int temp = array[begin-1];
            array[begin-1] = array[begin];
            array[begin] = temp;
            flag = false;
        }
    }
    if(flag) break;
}

注意：

只有在数据大部分都是有序的情况下才更能体现这个版本的优势，否则，可能会影响执行时间，因为都是乱序的情况下，这个版本还需要多执行指令。

（四）算法优化02
优化思路：

虽然算法优化01对特殊情况下已经改进了很多，但是毕竟这样的情况还是很少的。更多的可能是以下这种情况：序列尾部的数据已经局部有序了
那么这个时候，其实每次两两比较的时候就不需要在比较后面的数据了。也就是说，我们只要在第一个数据到局部有序数据的前面那一个之间进行两两比较就行,这样就能有效的减少比较的轮数，从而提高效率。

即：在每一次交换的时候都记录最后1次交换的位置，下一次在进行比较时，就只要在第一个到这个位置之间进行比较就行

代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int[] array =  {13, 23, 11, 15, 43, 54, 79};
		
for(int end=array.length-1; end > 0; end--) {
    int swapIndex = 1;
    for (int begin = 1; begin <= end; begin++) {
        if(array[begin-1] < array[begin]) {
            int temp = array[begin-1];
            array[begin-1] = array[begin];
            array[begin] = temp;
            swapIndex = begin;
        }
    }
    end = swapIndex;
}

四、选择排序

（一）算法思想

1） 从序列中找出最大的那个元素，然后与最末尾的元素交换位置（执行完一轮后，最末尾的那个元素就是最大的元素）；
2）忽略1）中曾经找到的最大元素，重复执行步骤1）
3）一共比较n-1轮

（二）算法实现
1
2
3
4
5
6
7
8
9
10
11
for(int end=array.length-1; end>0; end--) {
    int maxIndex = 0;
    for(int begin=1; begin<=end; begin++) {
        if(array[maxIndex] <= array[begin]) {
            maxIndex = begin;
        }
    }
    int temp = array[end];
    array[end] = array[maxIndex];
    array[maxIndex] = temp;
}

五、插入排序

（一）算法思想

1）将数据看做两部分：头部是已经排好序的，尾部是待排序的
2）从头开始扫描每一个元素，并将其插入到头部有序数据中的合适位置，使头部数据仍然保持有序。
3）关键在于如何找到合适的位置：将当前要插入的元素和前面的每一个元素进行比较，如果当前元素小于前一个元素，则交换；否则，说明已经到了合适的位置
4）重复执行，直到尾部数据全部插入完毕

（二）算法实现
1
2
3
4
5
6
7
8
9
for(int begin=1; begin<=array.length-1; begin++) {
    int cur = begin;
    while(cur>0 && array[cur-1]>array[cur]) {
        int temp = array[cur-1];
        array[cur-1] = array[cur];
        array[cur] = temp;
        cur--;
    }
}
（三）算法优化01
优化思想：

因为第一个版本是在找到一个比当前元素大的元素就需要进行交换，而交换一行要执行3条代码，这样的话，在逆序对比较多的情况下就需要执行很多条代码。那么针对这个情况，可以做如下优化：
1）先保存当前要插入元素的值；
2）用当前元素去和前面有序的元素进行比较，当有大于当前元素值的元素时，就将这个元素往后挪一个位置；
3）重复执行第2）步，直到找到一个元素小于当前要插入的元素即可；
4）将当前元素插入到空出的位置。
这样优化之后，在逆序对多的情况下相对于没优化之前，能非常有效的减小时间复杂度.

代码实现：
1
2
3
4
5
6
7
8
9
for(int begin=1; begin<=array.length-1; begin++) {
    int cur = begin;
    Integer value = array[cur];
    while(cur>0 && array[cur-1]>value) {
        array[cur] = array[cur-1];
        cur--;
    }
    array[cur] = value;
}
（四）算法优化02
优化思想：

因为在优化01中，我们是改进为挪位置，但是我们是每比较一次就挪动，这样其实中间一些重复的移动操作。
然后，我们发现，因为头部的数据是有序的，所以，我们可以使用二分搜索来进行优化：
1）使用二分搜索查找到当前元素可以加入的位置；
2）将这个位置及之后的所有元素往后移动一个位置；
3）将需要插入的数据插入到空出的位置。

代码实现：

在二分搜索算法更新之后，提供相关代码。

（五）时间复杂度

未优化 -> 优化01：减少了代码执行时间（因为需要执行的代码数量减少了）；
优化01 -> 优化02：减少了比较次数（因为之前是一个个比较，现在用二分）
但是，虽然说我们进行了两次优化，但是这其实只是在优化查找插入位置这一步，并不能降低时间复杂度。
因为，我们在进行插入时，还是需要挪动位置的，需要O(N)，然后又需要插入n个元素，
所以，不管怎样，时间复杂度都是O(N的平方)

六、快速排序

（一）算法思想

1）从序列中选择一个轴点元素（pivot）(一般每次选择 0 位置的元素为轴点元素)
2）利用 pivot 将序列分割成 2 个子序列
a. 将小于 pivot 的元素放在pivot前面（左侧）
b. 将大于 pivot 的元素放在pivot后面（右侧）
c. 等于pivot的元素放哪边都可以
3）对子序列进行1）、2） 操作，直到不能再分割（子序列中只剩下1个元素）
快速排序的重点在于如何确定轴点的位置，因为轴点的位置一旦确定，就能继续对左右两边继续进行快速排序。
确定轴点的步骤如下：
1）保存轴点的值；
2）首先从右边往左边扫描，如果当前值大于轴点值，那么end–，继续往左扫描；如果当前值小于等于轴点值，那么将当前值覆盖到begin位置，begin++，切换到从左往右扫描；
3）从左往右进行扫描，如果当前值小于等于轴点的值，那么begin++，继续往右扫描；如果当前值大于轴点元素，则将当前值覆盖到end位置，end–，切换到从右往左扫描；
4）重复执行2）、3）步，直到begin==end，此时除轴点外都排序完成，将轴点的值赋值到begin/end位置即可，并且begin/end就是轴点的位置。

（二）算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class Demo01 {
	public static void main(String[] args) {
		Integer[] array = {21, 34, 4, -1, 45, 56, 99, 1, 4, 67};
		quickSort(array, 0, array.length);
	}
	
	public static void quickSort(Integer[] array, int begin, int end) {
		//递归结束的条件：
		//1：只有一个，不需要排序
		//0：已经排序完毕
		if(end-begin < 2) return;
		
		int pivotIndex = pivotIndex(array, begin, end);
		//左边继续快速排序
		quickSort(array, begin, pivotIndex);
		//右边继续快速排序
		quickSort(array, pivotIndex+1, end);
	}
	
	/**
	 * 获取轴点的位置
	 * @return 轴点的位置
	 */
	public static int pivotIndex(Integer[] array, int begin, int end) {
		Integer pivot = array[begin];	  //保存轴点的值
		end--;							//end从length开始，所以先-1
		while(begin < end) {
			while(begin < end) {
				if(array[end] >= pivot) {
					end--;
				}else {
					array[begin++] = array[end];
					break;
				}
			}
			while(begin < end) {
				if(array[begin] <= pivot) {
					begin++;
				}else {
					array[end--] = array[begin];
					break;
				}
			}
		}
		array[begin] = pivot;
		return begin;
	}
}
（三）算法优化
优化思想：

1）因为每次的轴点元素都是默认选择第一个元素，这样的话，就有可能导致经过一遍排序之后元素都堆积在一边；

2）因为算法中的判断是如果当前元素等于轴点元素也是不会进行交换的，这样的话，如果所有元素都是相同的数据，就会导致在经过一遍排序之后都堆积在一边。

正对这两种情况，我们可以使用以下两个解决办法：

1）不使用固定的轴点元素，而是随机获取一个元素当做轴点元素；

2）在当前元素和轴点元素相等时，也进行交换。这样，如果元素都是相同的，那么也会被均匀的分配在轴点元素的两边。

代码实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class Demo02 {
	public static void main(String[] args) {
		Integer[] array = {21, 34, 4, -1, 45, 56, 99, 1, 4, 67};
		quickSort(array, 0, array.length);
	}
	
	public static void quickSort(Integer[] array, int begin, int end) {
		//递归结束的条件：
		//1：只有一个，不需要排序
		//0：已经排序完毕
		if(end-begin < 2) return;
		
		int pivotIndex = pivotIndex(array, begin, end);
		//左边继续快速排序
		quickSort(array, begin, pivotIndex);
		//右边继续快速排序
		quickSort(array, pivotIndex+1, end);
	}
	
	/**
	 * 获取轴点的位置
	 * @return 轴点的位置
	 */
	public static int pivotIndex(Integer[] array, int begin, int end) {
		//随机生成轴点元素索引
		int randomIndex = begin + (int)Math.random()*(end-begin);
		//将随机选取的轴点元素和begin位置元素进行交换
		int temp = array[begin];
		array[begin] = array[randomIndex];
		array[randomIndex] = temp;
		
		Integer pivot = array[begin];	  //保存轴点的值
		end--;							//end从length开始，所以先-1
		while(begin < end) {
			while(begin < end) {
				//不要写 >=，这样如果都是相等元素的话，会导致最坏情况的出现（推积在一边）
				//而如果只写 >，依然可以让元素均匀的分配在两边
				if(array[end] > pivot) {
					end--;
				}else {
					array[begin++] = array[end];
					break;
				}
			}
			while(begin < end) {
                //原理同上
				if(array[begin] < pivot) {
					begin++;
				}else {
					array[end--] = array[begin];
					break;
				}
			}
		}
		array[begin] = pivot;
		return begin;
	}
}

Java新手，若有错误，欢迎指正！

赏

都是码农，别客气了
| 阅读量次

扫一扫，分享到微信

微信分享二维码
本站总访问量: 本站总访客:

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

天下事有难易乎<br><br>为之，则难者亦易<br><br>不为，则易者亦难